Matlab如何求矩阵的秩

在matlab中求矩阵的秩是一项基本且常用的操作，对于数据分析、线性代数等领域的工作者来说至关重要。那么，究竟该如何在matlab里准确求出矩阵的秩呢？

一、使用rank函数

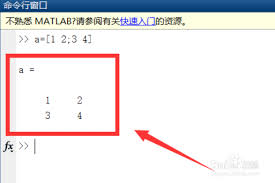
matlab提供了非常便捷的rank函数来计算矩阵的秩。假设我们有一个矩阵a，只需在命令窗口输入“rank(a)”，matlab就能快速给出矩阵a的秩。例如：

```matlab

a = [1 2 3; 4 5 6; 7 8 9];

rank_a = rank(a)

```

运行这段代码后，matlab会返回矩阵a的秩。

二、矩阵秩的意义

矩阵的秩反映了矩阵中线性无关的行向量或列向量的最大个数。它在很多方面有着重要意义。比如在求解线性方程组时，矩阵的秩可以帮助我们判断方程组解的情况。当系数矩阵的秩等于增广矩阵的秩且等于未知数的个数时，方程组有唯一解；当秩相等但小于未知数个数时，方程组有无穷多解；当秩不相等时，方程组无解。

三、实际应用案例

假设有一个图像数据矩阵，我们可以通过求其秩来分析图像的某些特征。例如，在图像处理中，矩阵的秩可能与图像的纹理复杂度等相关。通过计算不同处理阶段图像矩阵的秩，我们可以评估图像处理算法对图像结构的影响。

```matlab

image_matrix = imread('example.jpg');

gray_matrix = rgb2gray(image_matrix);

rank_image = rank(gray_matrix);

```

这里先将彩色图像转换为灰度图像，然后计算灰度图像矩阵的秩，从而了解图像在灰度层面的某种特征。

四、注意事项

在使用rank函数时，要确保输入的矩阵是有效的。如果矩阵元素包含非数值类型，matlab可能会报错。另外，对于非常大的矩阵，计算秩可能会消耗较多时间和内存，需要根据实际情况合理处理。

总之，掌握在matlab中求矩阵的秩的方法，能让我们在处理各种矩阵相关问题时更加得心应手，无论是学术研究还是实际工程应用，都有着重要的价值。